双指针技巧

双指针有两类：

• 快慢指针
  • 一般用于解决链表相关的问题，如判断链表是否存在环
• 左右指针
  • 一般用于解决数组相关的问题，如二分查找

快慢指针

快慢指针一般都初始化指向链表的头结点 head，前进时快指针 fast 在前，慢指针 slow 在后，巧妙解决一些链表中的问题。

判断链表中是否存在环

因为单链表的特点是每个节点只知道下一个节点，所以一个指针的话无法判断链表中是否含有环的。

使用快慢指针的思想解决链表中是否存在环的问题，其实是非常简单的，快慢指针初始时都指向链表头结点，慢指针每次前进一步，快指针每次前进两步。

• 如果链表不存在环，那么快指针最终会运行到链表的终端节点
• 如果链表存在环，那么快指针会多跑一会然后追上慢指针，此时说明链表存在环。

boolean hasCycle(ListNode head) {
    ListNode fast = head;
    ListNode slow = head;

    while(fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;

        if (fast == slow) {
            return true;
        }
    }
    return false;
} 

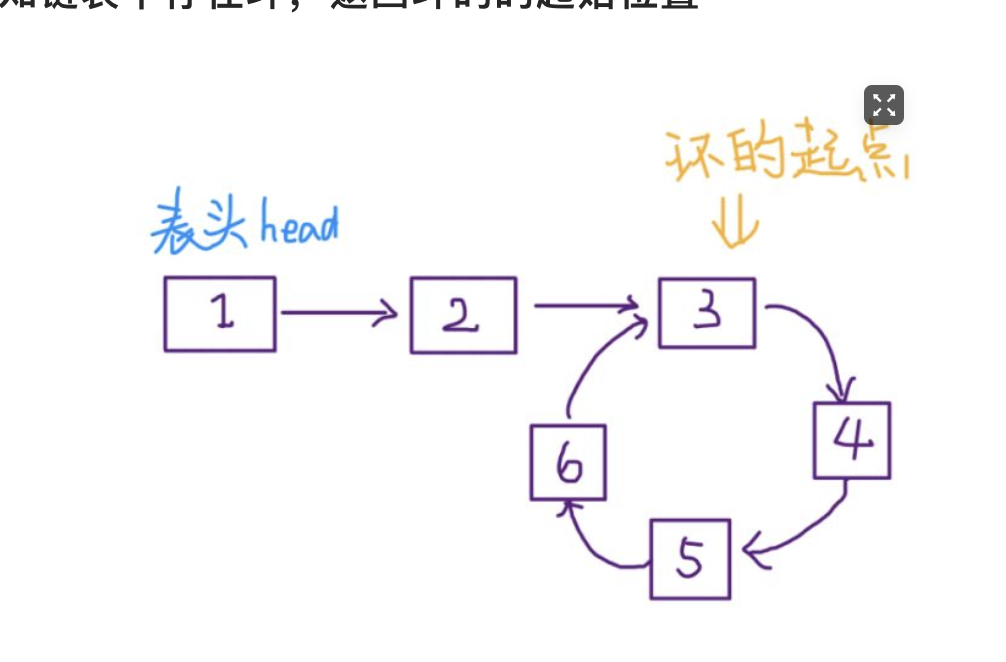
已知链表中存在环，返回环的的起始位置

< br />
关于计算环的起点这个，需要用到一点的数学知识，我们假定快慢指针在4这个位置相遇了。同时我们做如下约定：

• 表头1到环起点3之间的距离我们记录为m
• 节点3和节点4之间的距离我们记录为n
• 环的长度我们记录为r
• slow指针从表头1到当前位置4一共经过的距离我们记录为k

因此我们会有如下结论：

• slow指针走的距离为k, 我们很容易得出k=m+n，那么fast指针走的距离就会是2k, 假定相遇时fast走了p圈，所以fast指针走的距离为：m + pr + n
• 根据上一步的推理，我们会有如下的等式：pr + n + m = 2k = 2m + 2n
• 所以pr = m + n. 所以我们可以得出，节点4顺时针到节点3的距离为 pr - n = m。其实可以推断出p = 1的。所以节点4顺时针到节点3的距离和节点1到节点3的距离是相等的。因此我们的算法代码如下：

boolean getCycleStartPosition(ListNode head) {
    ListNode fast = head;
    ListNode slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;

        //第一次相遇推出循环
        if (fast == slow) {
            break;
        }
    }

    //将慢指针设置为起点，然后快慢指针都每次走一步
    slow = head;
    while(slow != fast) {
        slow = slow.next;
        fast = fast.next;
    }
    return slow;
}

寻找链表中间节点

这个问题的解法思路也是用快慢指针，期初2个指针都指向链表头部，然后慢指针每次走一步，快指针每次走两步，当快指针到达链表结尾时，慢指针的位置就是链表的中间节点。

ListNode getMidNode(ListNode head) {
    ListNode fast = head;
    ListNode slow = head;
    while(fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
    }
    return slow;
}

当链表的长度是奇数时，slow 恰巧停在中点位置；如果长度是偶数，slow 最终的位置是中间偏右

寻找链表的倒数第 k 个元素

这个问题换是快慢指针的事情，这次快慢指针都是每次走一步，但是得先让快指针提前走k步而已。

ListNode getLastKNode(ListNode head, int k) {
    if (head == null || k < 0) {
        return null;
    }
    ListNode fast = head;
    ListNode slow = head;

    for(int i = 0; i < k; i++) {
        fast = fast.next;
        if (fast == null) {
            return null;
        }
    }

    while(fast != null && fast.next != null) {
        fast = fast.next;
        slow = slow.next;
    }
    return slow;
}